In this note, we will look at how the peculiarity of quantum mechanics arise from a (relatively)
simple physics experiment. The goal is to create a more concrete thinking of the existence of quantum mechanics and an early introduction to the physical intuition of quantum mechanics. The simple set-up led to a series of conclusions and the formulation of the postulates of quantum mechanics, and most importantly, the necessity for the departure of quantum mechanics.
Adapted from J.J. Sakurai, Modern Quantum Mechanics
E&M Background
Similar to a electric dipole moment defined from charge configuration, a magnetic dipole moment can be defined from electric current and a vector area in the form of $\pmb{m} \equiv I \int d\pmb{a}$, with the direction given by the right hand rule. If the defined area is flat, the quantity is simply the product $Ia$. The physical intuition of the magnetic dipole is the torque exerted on an object per magnetic field; i.e. an object will rotate under a magnetic field until its magnetic dipole lines up with the direction of the field. Similar to the electric dipole, the magnetic dipole experiences an interaction energy $E = - \mu \cdot \pmb{B}$, and consequently a force $F = - \frac{\partial}{\partial s}(E) = \frac{\partial}{\partial s}(\mu \cdot \pmb{B})$ at direction $s$. The magnetic moment can also be associated with the classical angular momentum, for which we will call the orbital angular momentum $\pmb{L}$. Consider a point particle with charge $q$ and mass $m$ rotating about an axis with radius $r$, the relation is given by: \[\mu=IA= \frac{q}{T}\pi r^2=\frac{qvr}{2}=\frac{q}{2m}L\] where we used the quantities $T$ for the period $\frac{2\pi r}{v}$, $L$ for the orbital angular momentum $mvr$, and substituted $I = \frac{q}{T}$, $A=\pi r^2$. It turns out that the relationship between $\mu$ and $L$ is generally true, up to a constant of proportionality, whenever we consider a mass and charge in space. Hence, we can also let such objects rotate about an axis through its center - spinning, which we can give such special angular momentum a symbol: $S$, and a special name: spin. This simple classic picture of spin carries on in quantum mechanics, but as we move on, we will see that it is a complete different concept to grasp. For example, as we move to subatomic particles, e.g. electrons, they cannot actually spin in the classical sense as they do not have an axis (think wave-particle duality). Nonetheless, the spin remains a type of angular momentum, and the relation still holds, i.e. \[\pmb{S} \propto \pmb{L} \propto \pmb{\mu}\]
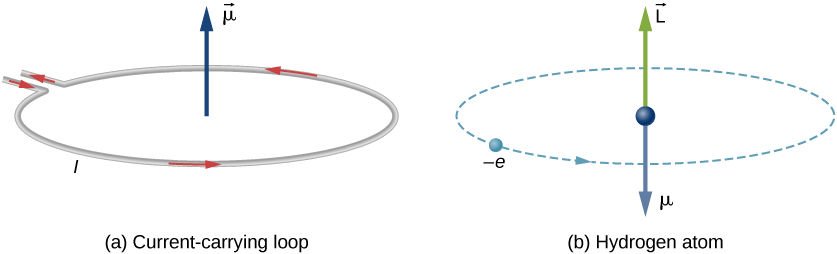
Origin of the magnetic dipole: Recall from electrostatics that the electric potential can be written as power series of $1/r$; a similar expansion can be done for the magnetostatic vector potential $\pmb{A}$, with the dipole moment term arising from the $1/r^2$ term. See Griffths, Introduction to Electrodynamics for more information.
Setup of the Experiment
We will begin with burning silver atoms in an oven, and proceed to dig a hole in the oven such that some heated silver atoms can be emitted as a beam subjected to an inhomogeneous magnetic field, specifically, $\nabla \pmb{B} < 0$. The resulting beam is then projected onto a screen for observation. The choice of silver is a subtle detail. Recall that the electron configuration of silver is $[\ce{Kr}]4d^{10}5s^1$. The filled d shell electrons contribute no net spin (think freshman chemistry), and the remaining lone electron contributes a magnetic moment $\mu$ to the silver atom, which by the previous relation, also gives the silver atom spin $\pmb{S}$.
As mentioned previously, there is a corresponding force $F$ with the magnetic moment $\mu$. For the sake of simplicity, we will only consider the z component of the force: $F_z = \frac{\partial}{\partial z}(\mu \cdot \pmb{B}) \approx \mu_z\frac{\partial}{\partial z}(B_z)$. Given the setup of the experiment where the gradient of the field is negative, silver atoms with $\mu_z > 0$ will experience a downward force and vice versa. For a beam with a random mixture of silver atoms with different $\mu_z$s, the screen will show the relative values of $\mu_z$s. Recall that $\mu_z \propto S_z$; we will reference the physicists that the constant of proportionality is $\frac{e}{m_ec}$. The absolute value here is not important, but notice that the constant is negative ($e < 0$). Therefore, the screen ultimately “measures” $\mu_z$s and $S_z$s of silver atoms, with the top of the screen (upward force) corresponding to $\mu_z < 0$ and $S_z > 0$ and vice versa.
Unexpected Results
Classically, the z component of $\mu$ is $\mu_z = |\mu| \cos(\theta)$, where $\theta$ is the angle between $\mu$ and the field axis. Furthermore, the silver atoms’ magnetic moments $\mu$ are randomly oriented as they are emitted from the oven; hence, classically, $\mu_z$ should take on a continuous range of values from $+|\mu_z|$ to $-|\mu_z|$. However, in reality, the screen only portraits two points. This is the beginning when scientists realized “quantization”, and the need of a new theory to explain the classically unexplainable result. It just so happens that we chose the z-axis, but after all, we could have chosen the x axis to orient the magnetic field, and the above results still hold. In such fashion, we will be expecting the beam to split into $S_x$ and $S_-x$. And in fact, it leads to the formulation of quantum mechanics.
Sequential Stern-Gerlach
Continuing our previous experiment, if we subject only the spin up ($S_z$) beam to the same apparatus, which we will name $SG\pmb{\hat z}$, blocking the spin down beam, we will get only one beam - $S_z$. This should make sense, since the atom’s spin up beam should remain spin up.
We could also arrange them to be a bit more interesting. Let the spin up beam enter an apparatus where the magnetic field is oriented in the $x$ axis, which we will name $SG\pmb{\hat x}$. Interestingly, the spin up beam does not remain spin up this time, but it split again into two beams of equal intensities. One might be inclined to think that 50% of the first spin up beam contained 50% $+S_z$ and 50% $+S_x$, while the remaining 50% contained another 50% $S_z$ and 50% $-S_x$. However, this would not explain the behaviour when a third apparatus is added. Let’s block off the spin down $-S_x$ beam, and only allow the spin up $S_x$ beam to enter another $SG\pmb{\hat z}$ apparatus. The result: the beam split again into $S_z$ and $-S_z$! How can the $-S_z$ reappear after we blocked it since the first apparatus?
This experiment illustrates a fact in quantum mechanics: we are not able to simultaneously determine both $S_z$ and $S_x$. And in fact, the second apparatus removed any previous information of $S_z$. A curious reader might draw connections of these pictures to the behaviour of a vector being “transferred” around in two vector spaces. In fact, such mathematical description lays the ground for quantum mechanics.